Padraig Corcoran
Regularization of Persistent Homology Gradient Computation
Nov 14, 2020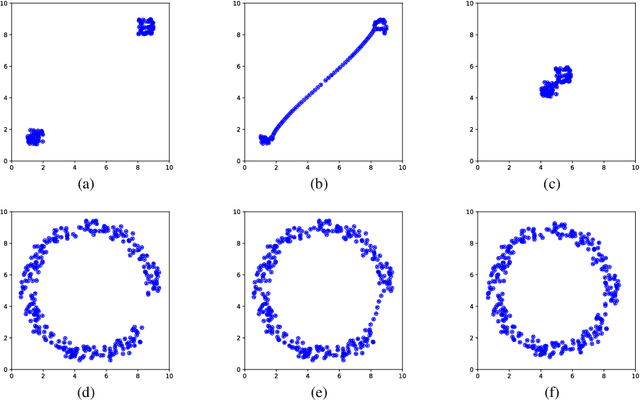
Abstract:Persistent homology is a method for computing the topological features present in a given data. Recently, there has been much interest in the integration of persistent homology as a computational step in neural networks or deep learning. In order for a given computation to be integrated in such a way, the computation in question must be differentiable. Computing the gradients of persistent homology is an ill-posed inverse problem with infinitely many solutions. Consequently, it is important to perform regularization so that the solution obtained agrees with known priors. In this work we propose a novel method for regularizing persistent homology gradient computation through the addition of a grouping term. This has the effect of helping to ensure gradients are defined with respect to larger entities and not individual points.
An End-to-End Graph Convolutional Kernel Support Vector Machine
Feb 29, 2020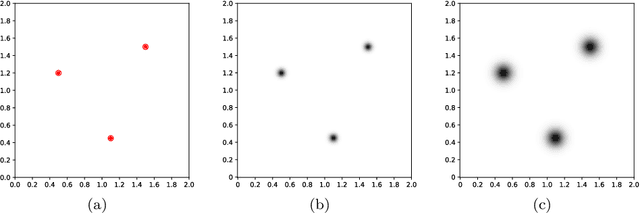
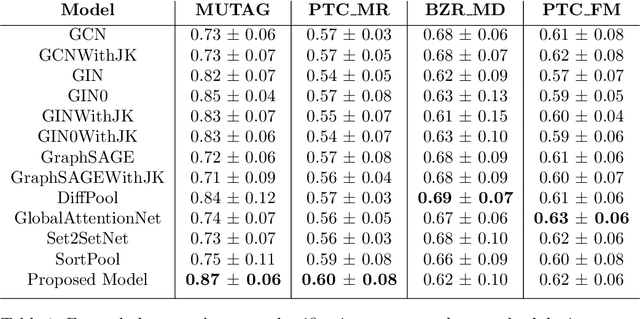
Abstract:A novel kernel-based support vector machine (SVM) for graph classification is proposed. The SVM feature space mapping consists of a sequence of graph convolutional layers, which generates a vector space representation for each vertex, followed by a pooling layer which generates a reproducing kernel Hilbert space (RKHS) representation for the graph. The use of a RKHS offers the ability to implicitly operate in this space using a kernel function without the computational complexity of explicitly mapping into it. The proposed model is trained in a supervised end-to-end manner whereby the convolutional layers, the kernel function and SVM parameters are jointly optimized with respect to a regularized classification loss. This approach is distinct from existing kernel-based graph classification models which instead either use feature engineering or unsupervised learning to define the kernel function. Experimental results demonstrate that the proposed model outperforms existing deep learning baseline models on a number of datasets.
Deep Q-Learning for Directed Acyclic Graph Generation
Jun 05, 2019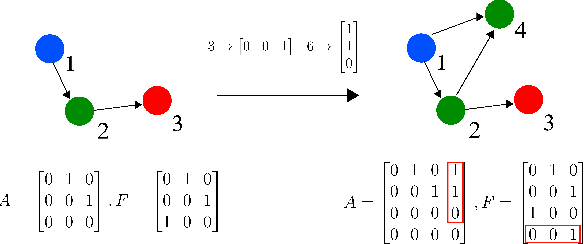
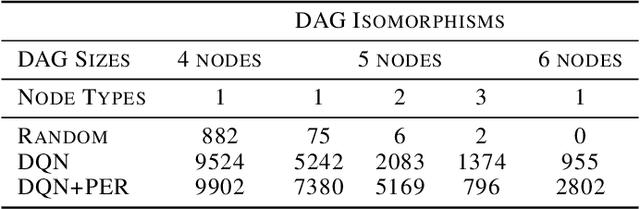
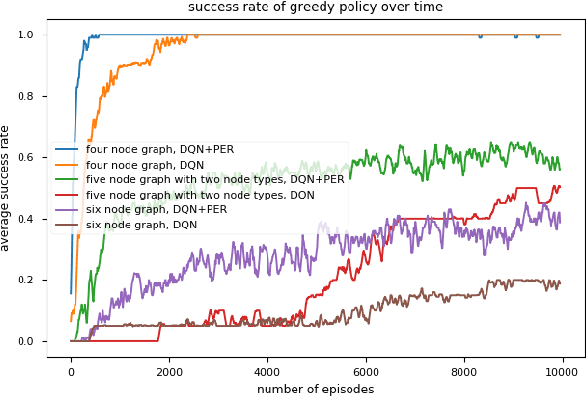
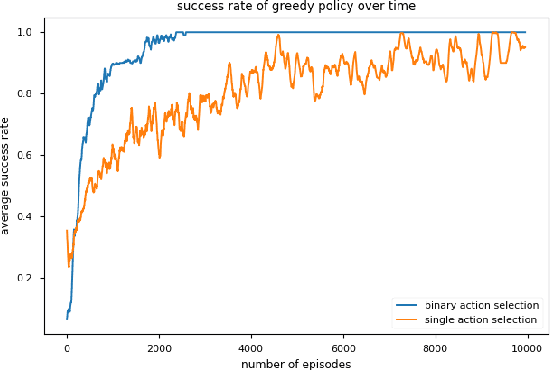
Abstract:We present a method to generate directed acyclic graphs (DAGs) using deep reinforcement learning, specifically deep Q-learning. Generating graphs with specified structures is an important and challenging task in various application fields, however most current graph generation methods produce graphs with undirected edges. We demonstrate that this method is capable of generating DAGs with topology and node types satisfying specified criteria in highly sparse reward environments.
Function Space Pooling For Graph Convolutional Networks
May 15, 2019

Abstract:Convolutional layers in graph neural networks are a fundamental type of layer which output a representation or embedding of each graph vertex. The representation typically encodes information about the vertex in question and its neighbourhood. If one wishes to perform a graph centric task such as graph classification the set of vertex representations must be integrated or pooled to form a graph representation. We propose a novel pooling method which transforms a set of vertex representations into a function space representation. Experiential results demonstrate that the proposed method outperforms standard pooling methods of computing the sum and mean vertex representation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge